It probably won’t be you
An interactive exploration of our lottery instincts.
I was 16 when I bought my first lottery scratch card. I was waiting for a bus and had just enough money for the fare, but I was thirsty and wanted a drink from the nearby shop. I decided to gamble my bus fare on a scratch card. I thought I’d win £10 (at the very least) and could then gorge myself on sweets and fizzy drinks before the bus arrived.
I walked home, thirsty and swore never to buy a lottery ticket again.
Lousy instincts
We all know what a 1 in 2 chance feels like; we’ve tossed a coin. We know what it’s like to roll a dice or draw an ace of spades from a deck of cards. Most of us have some feel of these odds.
Try them below...
Didn’t draw many cards right?
It only takes odds over 1 in 50 to feel that your chances are slim. Climb the odds ladder higher into thousands and millions, and our instincts are totally spent.
But it’s still possible to win, right? ... right?!
Dopamine strikes
To most people, the lottery isn’t just odds. A whole party of emotions is wrapped up in the drama of buying, dreaming and checking your numbers. Spikes of dopamine override our caution. We overestimate the possibility of reward and feel good about it, ensuring we return for more.
The chance of matching all six numbers in the UK is 1 in 45,057,474. This means nothing to most people. It’s impossible to get the feel for these odds, so we don’t - we dream instead.
But matching three numbers is only 1 in 97 - that’s not bad. And you win £30 at just £2 a pop. Let’s see what that feels like...
How did you do? You spent a lot more than you won, didn’t you? You’re starting to get a feel for it now.
The numbers
Matching more than four numbers takes us past the realms of clickability, so we’re going to simulate playing the lottery twice a week until you die.
Start by choosing your favourite six numbers…
I’m sure you paused for a moment to consider your choices. You may have even chosen numbers that mean something to you; your mother’s birthday, an anniversary, perhaps? This made you feel in control of your destiny.
The truth is, you might as well have chosen 1,2,3,4,5,6, which has precisely the same odds as any combination of six numbers. But you’d be an idiot to choose those right? - Now you're getting it.
Your numbers work against you
In October 2022, a record 433 people won the jackpot in the Philippines. They all chose the same numbers consisting of multiples of nine; 9, 18, 27, 36, 45, 54 - a pattern that many people play.
The same thing happened in the UK with multiples of seven. A whopping 4,082 winners received only £15 each for matching five balls while matching only three would have won them £25.
Choosing your own numbers allows you to construct your own divine narrative around winning, but it also works against you. Numerical patterns and dates can actually increase the chance of sharing the prize with others.
Prize breakdown
Let’s take a moment to look at the prizes offered in the UK.
| Matching | Odds | Prize |
|---|---|---|
| 3 balls | 1 in 97 | £30 |
| 4 balls | 1 in 2,180 | £140 |
| 5 balls | 1 in 144,415 | £1,750 |
| 5 balls + bonus ball | 1 in 7,509,579 | £1,000,000 |
| 6 balls | 1 in 45,057,474 | £7,500,000 |
And if we plot those on a chart, you can see how disproportionate they are...
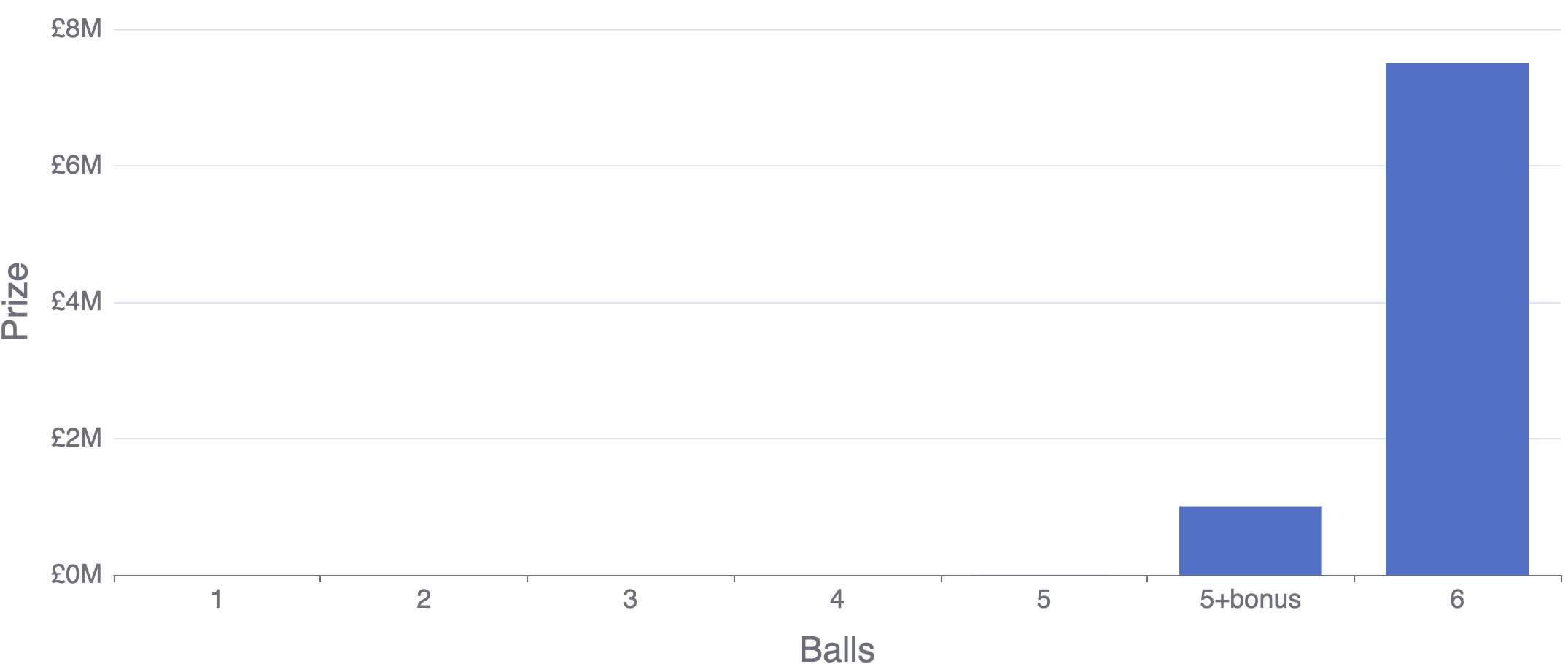
The only life-changing prizes are the top two. Matching five balls wins around 0.02% of the jackpot—it doesn’t even register on the chart. If you want to see a bar for five-ball matches, we would need to render this chart at least 6000px high.
Ok, I’m feeling lucky, let’s roll!
As a year old, there’s around 6240 draws to left play before you die (If you play twice a week, based on UK life expectancy).
So let’s simulate your precious numbers from earlier, playing twice a week, for the rest of your life. Fingers crossed!
The simulator above has played 0 tickets for 0 online players. 0 players made a profit, and 0 players matched all six numbers to win the jackpot.
The Gambler’s Fallacy
If you go a long time without winning, you may feel you are “due” to win. This is incorrect, as we know that each draw is independent and doesn’t affect the probability of the next one.
It can be confusing because there are two probabilities at work in your mind...
- The independent probability of hitting the jackpot remains 1 in 45,057,474 regardless of past events.
- The cumulative probability taking into account the nature of repeated independent events. So collectively there is a higher chance of winning at least once.
For example, a single dice roll has a 16.66% (1 in 6) chance of landing a six. But if you rolled nine times and hadn’t rolled a six, you’d start sensing cumulative probability; in this case, 84% chance that ten rolls would roll at least one six.
This is the delusion of the Gambler’s Fallacy, as there is still only a 16.66% (1 in 6) chance of rolling a six. Although it's counterintuitive, the odds of winning next are the same as they’ve always been.
Back to the lottery - any sense of cumulative probability among such high odds is just your mind playing tricks. With finite years and a limited budget, you’ll never experience it unless we increase your lifespan. So let's try that - use the slider below to calculate a cumulative probability.
Or, if you want to simulate cumulative probability in this lifetime, you could increase the number of tickets you play per draw...
Remember, the jackpot is only £7,500,000. Spending this amount on tickets gives you around a 1 in 13 chance of settling your debt.
Conclusion
Hopefully, you've now got a feel for your chances when the odds are incredibly high, instead of relying on bad intuition.
When the odds are lower than the turns you can easily take, you can get a valuable sense of winning. But it's a lot tougher when they are higher and restricted by time and money, like the lottery.
Footnotes
- Binomial distribution probability mass function (PMF) from stdlib
- Read more about the Gambler's fallacy